Practical - 02
AIM: Design a Finite State Machine (FSM) that accepts all strings over input symbols {0, 1} which are divisible by 3.
Discussion:
As per the AIM, set of valid strings are represented by set A:
A = {0, 00, 000, 11, 011, 110, ...}
means any binary string that when divide by three gives remainder zero.
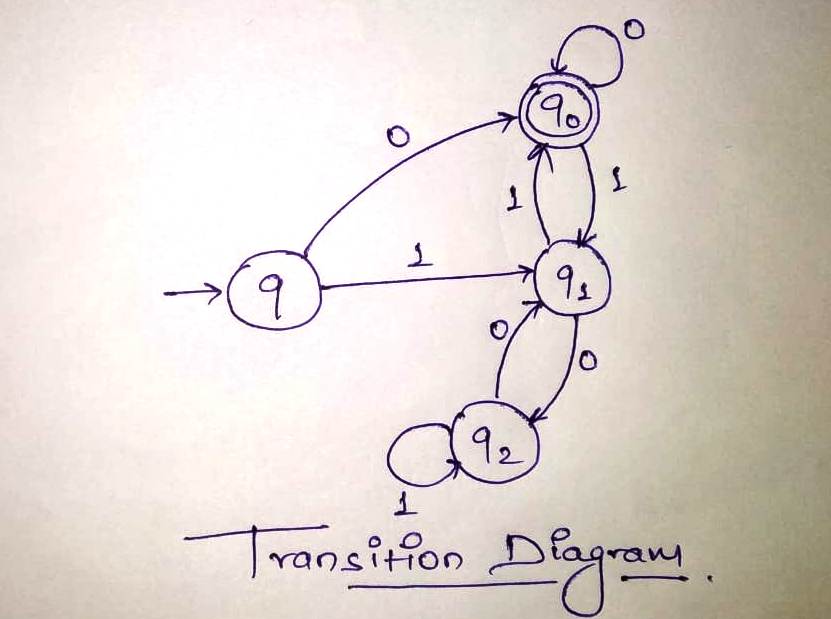
Let M be the machine for above AIM, hence it can be define as M(Q, Σ, 𝛿, q0, F)
where
Q: set of states: {q, q0, q1, q2}
Σ: set of input symbols: {0, 1}
q0: initial state (q)
F: set of Final states: {q0}
𝛿: Transition Function: (Transition state diagram is shown in Figure 1.)
| - | ||
| q | q0 | q1 |
| q0 | q0 | q1 |
| q1 | q2 | q0 |
| q2 | q1 | q2 |
Code in C++
#include <iostream.h>
#include <conio.h>
#include <stdio.h>
void main()
{
char Input[100];
clrscr();
cout<<"Enter a string to validate (input string should be of 0 and 1)\n";
gets(Input);
int i=-1;
q:
i++;
if(Input[i]=='0')
{
goto q0;
}
else if(Input[i]=='1')
{
goto q1;
}
else if(Input[i]=='\0')
{
goto Invalid;
}
else
{
goto Wrong;
}
q0:
i++;
if(Input[i]=='0')
{
goto q0;
}
else if(Input[i]=='1')
{
goto q1;
}
else if(Input[i]=='\0')
{
goto Valid;
}
else
{
goto Wrong;
}
q1:
i++;
if(Input[i]=='0')
{
goto q2;
}
else if(Input[i]=='1')
{
goto q0;
}
else if(Input[i]=='\0')
{
goto Invalid;
}
else
{
goto Wrong;
}
q2:
i++;
if(Input[i]=='0')
{
goto q1;
}
else if(Input[i]=='1')
{
goto q2;
}
else if(Input[i]=='\0')
{
goto Invalid;
}
else
{
goto Wrong;
}
Valid:
cout<<"\n Output: Valid String";
goto exit;
Invalid:
cout<<"\n Output: Invalid String";
goto exit;
Wrong:
cout<<"\n Please enter binary string {format of 0, 1}";
exit:
getch();
}